Conway's Game of Life–A Remembrance
Jun 7, 2020
Most of us played with Lego blocks or jigsaw puzzles when we were kids–maybe you still do. You remember spending hours tinkering and rearranging them into different shapes and structures. Our imagination was the limit. These are very simple things: pieces of plastic and paperboard in a few different shapes that snap together. Taken by themselves, they are dull and boring. Yet, we were entertained for long periods. But it's not the individual parts that make them fun and interesting. It's the thinking–about how we can arrange them–and the building, creating something new that entertains us. The potential in simple things is fascinating.
Lego blocks and jigsaw puzzles are not the only things that are simple, yet fascinating. Conway's Game of Life falls in this category. The game is a cellular automaton–a grid of cells that take a specific state, for example, "on" or "off." It was created by British mathematician John Horton Conway in 1970. That same year–when Martin Gardner featured the game in an article in Scientific American–it became an instant sensation.
The Game of Life
The Game of Life–or simply Life, as Conway called it originally–consists of a two-dimensional grid of squared cells. Conway borrowed a board of the game Go when creating Life.
Each cell is either "alive" (populated) or "dead" (unpopulated). A cell has eight neighbors–these are the eight squares surrounding the cell.
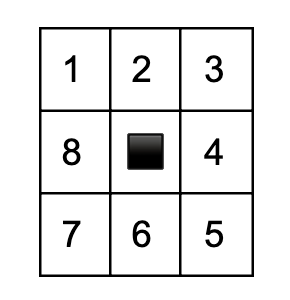
A cell in the center, with eight neighbors.
To start the game we choose an initial configuration of the cells. Then, in the next period, all cells update their state based on the following rules:
- A live cell with two or three live neighbors stays alive
- A dead cell with three live neighbors becomes alive
- All other live cells die (and dead cells stay dead)
That's it. These are all the rules of the Game of Life. The game is a zero-player game, meaning it doesn't require any players to proceed. The game advances, updating the cells, giving birth to new generations.
The fun part is picking the initial arrangement and then watching what happens. Depending on how we choose, patterns emerge–they can get complex, and it's mesmerizing watching the cells rearranging themselves. Some configurations die out after a few generations, others remain still, while others go out producing different patterns and then come back to the original configuration, creating a cycle. It all depends on that initial arrangement. We better choose carefully.
The Game of Life can also generate randomness–patterns that show unpredictable behavior. In some cases, it's impossible to tell if a pattern will perish or continue to live forever. This is known as the halting problem. As John Conway puts it: "it's not a question of not being able to tell because you haven't got a big enough brain, it's an absolute condition–it doesn't matter how clever you are." This consequence is fascinating, given that the game is governed only by three simple rules.
Let's Play
Well-known configurations exist in the Game of Life. The blinker is a straight line of three adjacent cells. It switches between horizontal and vertical positions every period.

Blinker
The glider is a pattern that travels diagonally across the grid.

Glider
A more complex configuration, Gosper's glider gun, generates gliders.
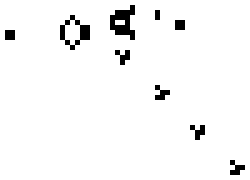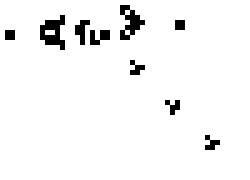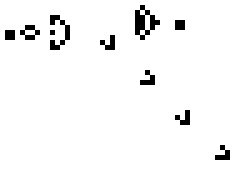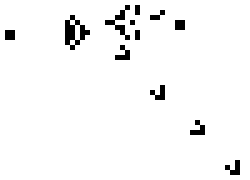
Gosper's Glider gun (credit: Lucas Vieira / CC BY-SA)
There are many more patterns with varying degrees of complexity.
When Conway created the game, he used a board of Go as the grid–he had no computers. But, now we can use computer programs to see the patterns evolve. Given the simplicity of its rules, it's easy to program the Game of Life. The code below implements a basic game with a glider. I made a few adjustments to consider the cells at the edges of the grid–they will have less than eight neighbors. In the game, the grid is infinite.
#!/usr/bin/env python3
""" Conway's Game of Life
"""
import copy
def game_of_life(grid_size, periods):
curr_grid = [[0]*grid_size for _ in range(grid_size)]
next_grid = [[0]*grid_size for _ in range(grid_size)]
init_setup(curr_grid)
for tick in range(periods):
next_grid = next_state(curr_grid, next_grid)
curr_grid = copy.deepcopy(next_grid)
print("Period: {}".format(tick+1))
print_grid(curr_grid)
def next_state(curr_grid, next_grid):
size = len(curr_grid)
alive = False
field_sum = 0
for r in range(size):
for c in range(size):
if r > 0:
field_sum += sum(curr_grid[r-1][c-1:c+2])
field_sum += sum(curr_grid[r][c-1:c+2])
if r < size-1:
field_sum += sum(curr_grid[r+1][c-1:c+2])
if curr_grid[r][c] == 1:
alive = True
field_sum -= 1 #count neighbors only
if alive and (field_sum > 1 and field_sum <= 3):
next_grid[r][c] = 1
elif not alive and field_sum == 3:
next_grid[r][c] = 1
else:
next_grid[r][c] = 0
field_sum = 0
alive = False
return next_grid
def init_setup(curr_grid):
#set up a "glider"
curr_grid[1][3] = 1
curr_grid[2][1] = 1
curr_grid[2][3] = 1
curr_grid[3][2] = 1
curr_grid[3][3] = 1
print_grid(curr_grid) #print the initial state
def print_grid(grid):
for i in range(len(grid)):
print(grid[i])
print("\n")
def main():
""" Start Game of Life with a 10x10 grid, and run it for 20 periods
"""
game_of_life(10, 20)
if __name__ == '__main__':
main()
The ConwayLife website contains more resources and a free program to explore the Game of Life.
A Life Well Played

Dr. John Conway in 2005. (credit: Thane Plambeck / CC BY)
Last April, John Conway died of COVID-19 in New Brunswick, New Jersey, at the age of 82. Born in Liverpool, England, Conway obtained his Ph.D. in mathematics from the University of Cambridge, where he also was a lecturer. He later became Chair of Mathematics at Princeton University in New Jersey. He was a Fellow of the Royal Society and won numerous awards in mathematics.
His contributions to the field are numerous. Spanning into the areas of knot theory, number theory, finite groups, combinatorial game theory, and coding theory. Conway enjoyed playing games–such as backgammon–and magic tricks. Together with a colleague invented the paper-and-pencil game Sprouts. Of course, he also gave us the Game of Life.
We are forever thankful to him for sparking our imaginations and showing the world that math is fascinating and fun. May he rest in peace.
Bonus:
Video of John Conway talking about inventing the Game of Life.
