Thoughts On Game Theory

Oct 11, 2021

---

Game theory can help us determine the best course of action when facing a situation requiring strategic thinking. Economics and other social sciences such as psychology and political science use game theory extensively. Computer science applies game theory to develop artificial intelligence algorithms. Also, cryptocurrencies and blockchain applications follow game-theoretic rules (I wrote more about this here). Game theory uses mathematical techniques to analyze and find the optimal strategy for a player or agent to follow. We'll see what finding the optimal strategy means.

This may sound like a powerful tool to have. But, given the complexities of some games, game theory is still limited. It can only give us a rough model of a given situation. Some of these models, although imperfect, can still be useful to gain a better understanding of a situation and help us in decision making.

Next, I'll describe basic game theory concepts, give some examples of its applications, and discuss its limitations. I will also make the case of why studying game theory is still worthwhile. After all, in many situations in life, having even a little bit of advantage can make a huge difference in whether we succeed or fail.

A Quick Intro to Game Theory

The field of game theory was established by John von Neumann in 1928 when he published the paper On the Theory of Games of Strategy. In 1944, von Neumann and Oskar Morgenstern co-authored the book Theory of Games and Economic Behavior–one of the foundational books on the subject. In game theory, we try to find the best strategy (or set of strategies) when faced with a situation involving one or more players and a potential payoff. In some cases, we can think of finding the best strategy as a mathematical optimization problem.

To model and analyze a game, we need to define a few things first. We need to know the number of players–the simplest (and still interesting) games are two-player games. As we add players, the analysis becomes more complex. Also, we need to know what actions the players can take. Then we need to establish the timing of the interactions. I.e. are the actions taken simultaneously or sequentially, and what is the order for each player? Finally, we specify the payoff to each player as a result of the interactions. These can be an economic incentive or some other kind of benefit expressed quantitatively. Once all this is defined, we can proceed with the analysis of the game.

For simplicity, we'll only look at two-player games to describe the basic concepts of game theory¹.

Unfortunately, game theory wouldn't have been very useful to play "green light/red light" (scene from Netflix TV show Squid Game - copyright: Netflix).

A payoff matrix is a useful tool to analyze games. The payoff matrix consists of a table containing the payoffs for each player when choosing a given strategy. The row numbers index the payoff for one player, while the column numbers index the other player's payoffs. When a game is represented as a payoff matrix, it's said to be in normal form. The table below is an example of a payoff matrix.

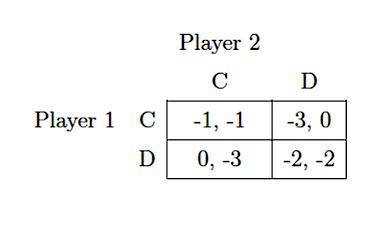
The payoffs for player 1 are the first number in the pairs inside each cell. The payoffs for player 2 are the second number in the pairs. Notice that player 1 is the row player while player 2 is the column player. The letters C and D indicate the name of the strategy (we'll use these in the examples in the following section).

What this tells us is the following. If player 1 chooses strategy C and player 2 chooses strategy D, their respective payoffs are -3 and 0 (the pair in the upper right corner of the matrix). As you can see, we can use this table to find the best strategy for each player in terms of payoffs.

Examples of Games

A popular example in game theory is the Prisoner's dilemma. The game is presented as follows. The two players committed a crime, and the police is interrogating them. As usual, they are in different rooms with no communication between them. The prosecutor offers each of them the following options. If you confess against the other player and the other player doesn't confess, then you get freed. If both players confess, then they both get a sentence of 2 years in prison. If you don't confess, but the other player does, you get convicted with a maximum sentence of 3 years in prison. If neither player confesses, they both get charged with the minimum sentence of 1 year in prison.

The payoff matrix looks like this:

Looking at the matrix, strategy C means to cooperate with the other player and not confess. Strategy D means to defect and confess to the prosecutor. The payoffs represent the number of years in prison (hence the negative sign). It's easy to see the following: if both players cooperate, i.e. they chose strategies (C, C), they both get the minimum sentence of 1 year in prison. If both of them defect–strategies (D, D)–they get the worst sentence of 2 years in prison. However, if one player acts purely on self-interest, they can avoid prison time provided the other player doesn't confess.

A purely rational player will always try to maximize its payoff. So–given that players don't know the action of the other one when making the decision–the strategy with the best payoff is to defect. This means that both players will choose strategy D and get the worst outcome than if they had chosen to cooperate. Hence the dilemma: the rational or optimal strategy is to defect, while cooperation is not optimal, even though it can result in a better payoff.

We can have different types of games, depending on the rules of play and payoffs. These games will have different properties with different optimal strategies. For example, in a coordination game, the optimal strategy is to coordinate with the other player to get the best outcome.

The payoff matrix below represents an example of the stag hunt game.

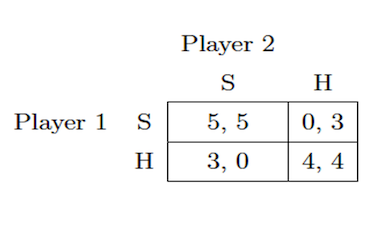
In this example, players 1 and 2 are hunters out in the forest, and they can either hunt for a stag (strategy S) or look for hares (strategy H). Successfully getting a stag is a two-hunter effort. However, both hunters are separated in the forest, so they can't communicate with each other. From the payoff matrix, we can see that the strategies with the highest payoff are (S, S). The second best would be (H, H). So, as long as both hunters choose the same action, their payoffs are maximized.

Nash Equilibrium

Strategies (S, S) and (H, H) above are what we call Nash equilibria². In game theory, the Nash equilibrium is the strategy–or set of strategies–in which every player's strategy is optimal when we hold the other player's strategy constant. To illustrate, consider that you're player 1 in the stag hunt game above. Then if you "fix" the player's 2 strategies to H, your best response–which will maximize your payoff–is to also play H. If you then fix the player's 2 strategies to S, your best response is to play strategy S.

This means that, when we find the Nash equilibrium strategy (or set of strategies), then playing any other strategy is suboptimal. However, not all games have a Nash equilibrium. In that case, we need to look for a mixed strategy, which usually involves choosing among several available strategies.

On the left is mathematician John F. Nash, who introduced the concept of the Nash equilibrium. He won the Nobel prize in Economics in 1994. On the right is actor Russell Crowe as John Nash in the movie A Beautiful Mind. (image source: New Atlas)

The examples above are just a peek at game theory. There's still a vast set of concepts left untouched. If you'd like to keep exploring the subject, I recommend some further readings at the end of this post.

Limitations of Game Theory

There are important limitations we should be aware of when using the tools of game theory. In general, when we try to create a model–e.g. to describe physical phenomena, financial markets, human behavior, etc.–it's almost impossible to capture every detail. This will always make our models inaccurate.

When representing a real-life situation with a game-theoretic model, we have to make several assumptions. For example, we assume that players always act rationally–this is known as the rational-agent model. In some cases, when we assign a value to the payoffs, they may be inconsistent with the preferences of some players. In reality, these assumptions may not hold, but we need them to simplify our analyses.

In his book, Thinking, Fast and Slow, Daniel Kahneman³ makes the point against the validity of the rational-agent model when dealing with human players. He distinguishes between purely rational and human agents, calling the former Econs, and the latter simply Humans. We as humans have different biases and preferences that influence our actions–more often than not, these actions are not completely rational.

As I mentioned above, a critical assumption we make in some games is in the assignment of quantitative values to the payoffs. The outcome of playing one strategy may be more appealing for one player than another. This includes the possibility of loss aversion, which will bias the preference for one strategy over another–even when the payoffs are asymmetric. I.e. one is much better than the other, but the better outcome involves taking a greater risk (e.g. losing a significant amount of money). In these types of situations, it's quite difficult to assign a value to a payoff that will work for all players.

Why Study Game Theory?

Besides these serious limitations, game theory is still valuable. It provides a framework to organize our thinking. We can combine game theory with other tools for better decision-making.

It seems to me, the most important aspect of studying game theory is that it forces us to put ourselves in the shoes of the other players–to understand what their available strategies are, and therefore better understand their point of view. Many times, this will lead us to discover flaws in our thinking.

---

Additional readings on Game Theory:

• Theory of Games and Economic Behavior – Written by John von Neumann and Oskar Morgenstern, who established the field of game theory.

• The Compleat Strategyst by J.D. Williams – The content is a bit outdated, but it serves as a wonderful (mostly non-technical) introduction to the subject.

• The Model Thinker by Scott E. Page – Chapter 4: Modeling Human Actors, provides a good overview of the rational-agent model.

Notes